2D 激光雷达 SLAM 中的实时回环检测

标签

cartographer

SLAM

paper

字数

8949 字

阅读时间

38 分钟

本论文翻译自 Real-Time Loop Closure in 2D LIDAR SLAM

作者： Wolfgang Hess , Damon Kohler, Holger Rapp, Daniel Andor （所有作者均来自谷歌）

Hess W, Kohler D, Rapp H, et al. Real-time loop closure in 2D LIDAR SLAM[C]//2016 IEEE international conference on robotics and automation (ICRA). IEEE, 2016: 1271-1278.

摘要

便携式激光测距仪（以下简称激光雷达/LIDAR）与同步定位与地图构建（SLAM）技术是获取竣工平面图的高效方法。实时生成并可视化平面图有助于操作人员评估采集数据的质量和覆盖范围。构建便携式采集平台需在有限的计算资源下运行。本文提出一种应用于背包式测绘平台的方法，该方法能够以 5cm 的分辨率实现实时测绘与回环检测。为达成实时回环检测，我们采用分支定界法计算扫描与子图的匹配结果作为约束条件。实验结果及与其他主流方法的对比表明，该方法在精度方面与现有成熟技术具有竞争力。

一、引言

竣工平面图在多种应用场景中具有重要价值。用于建筑管理任务的数据采集手动测量方法通常结合计算机辅助设计（CAD）与激光测距仪，这类方法效率低下，且由于依赖人类对建筑为直线集合的先验认知，往往无法准确描述空间的真实形态。借助 SLAM 技术，能够快速、精准地对大规模、复杂结构的建筑进行测绘，其效率较手动测量提升数个数量级。

SLAM 技术在该领域的应用并非全新理念，也不是本文的研究重点。本文的核心贡献是提出一种新型方法，用于降低基于激光测距数据计算回环约束的计算开销。该技术使我们能够对数万平方米的大型楼层进行测绘，同时为操作人员实时提供完全优化的结果。

二、相关工作

在基于激光雷达的 SLAM 方法中，扫描与扫描匹配（scan-to-scan matching）常被用于计算相对位姿变化^[1][2][3][4]。然而，仅依靠扫描与扫描匹配会快速累积误差。

扫描与地图匹配（scan-to-map matching）有助于抑制误差累积。例如，文献^[5]提出一种基于高斯-牛顿法(Gauss-Newton)的方法，在线性插值地图上寻找局部最优解。当通过高数据率激光雷达获得足够精确的位姿初始估计时，局部优化的扫描与地图匹配具有高效性和鲁棒性。在不稳定平台上，可利用惯性测量单元（IMU）估计重力方向，将激光扫描扇面投影至水平面。

像素级精确扫描匹配方法（如文献^[1:1]）进一步降低了局部误差累积。尽管计算开销更高，但该方法同样适用于回环检测。部分方法通过匹配激光扫描提取的特征来降低计算成本^[4:1]。其他回环检测方法包括基于直方图的匹配^[6]、扫描数据中的特征检测以及机器学习方法^[7]。

解决剩余局部误差累积的两种常用方法是粒子滤波（particle filter）和基于图的 SLAM（graph-based SLAM）^[2:1]、^[8]：

• 粒子滤波：需在每个粒子中维护完整的系统状态表示。对于基于栅格的 SLAM，当地图规模扩大时（例如，我们的一个测试案例为轨迹长度3km、面积22000m²的场景），计算资源消耗会迅速增加。文献^[9]提出采用低维特征表示方法，无需为每个粒子维护栅格地图，从而降低资源需求。当需要实时更新的栅格地图时，文献^[10]提出计算子图的方法，仅在必要时更新子图，最终地图通过所有子图的栅格化得到。
• 基于图的方法：通过节点集合表示位姿和特征，图中的边表示由观测生成的约束。可采用多种优化方法最小化所有约束引入的误差^[11]、^[12]。文献^[13]描述了一种适用于室外 SLAM 的系统，该系统结合基于图的方法、局部扫描与扫描匹配以及基于子图特征直方图的重叠局部地图匹配。

三、系统概述

谷歌的 Cartographer 系统以配备传感器的背包形式提供室内实时测绘解决方案，能够生成分辨率为 $r=5\text{cm}$ 的二维栅格地图。操作人员在建筑物内行走时，可实时查看正在生成的地图。激光扫描数据被插入到最佳估计位置对应的子图中，该位置在短时间内被认为具有足够的准确性。扫描匹配基于近期子图进行，仅依赖最新的扫描数据，因此世界坐标系下的位姿估计误差会逐渐累积。

为在中等硬件配置下实现良好性能，我们的 SLAM 方法未采用粒子滤波。为应对误差累积问题，系统定期执行位姿优化。

1. 当子图构建完成（即不再插入新的扫描数据）后，该子图将参与回环检测（loop closure）的扫描匹配过程；
2. 所有已完成的子图和扫描数据都会被自动纳入回环检测考虑范围，若根据当前位姿估计判断二者距离足够近，扫描匹配器将尝试在子图中寻找对应的扫描数据；
3. 如果在当前估计位姿周围的搜索窗口内找到足够优的匹配结果，则将其作为回环约束（loop closing constraint）添加到优化问题中；
4. 通过每几秒执行一次优化，操作人员在重访某个位置时能够实时实现回环检测。

为满足软实时（soft real-time）要求，回环扫描匹配的执行速度必须快于新扫描数据的生成速度，否则会出现明显的滞后。我们通过采用分支定界法（Branch-and-Bound Approach）以及为每个已完成子图预计算多个栅格（precomputed grids）的方式，满足了这一要求。

四、局部二维 SLAM

我们的系统结合了局部和全局两种独立的二维 SLAM 方法。两种方法均优化激光雷达观测（以下简称扫描）的位姿 $\xi =({\xi }_x,{\xi }_y,{\xi }_{\theta })$ ，其中 $(x,y)$ 表示平移量， ${\xi }_{\theta }$ 表示旋转角度。在背包等不稳定平台上，利用 IMU 估计重力方向，将水平安装的激光雷达扫描数据投影至二维世界坐标系。

在局部方法中，每帧连续扫描数据与世界地图的一个小片段（称为子图 $M$ ）进行匹配，通过非线性优化使扫描数据与子图对齐（该过程称为扫描匹配）。扫描匹配会随时间累积误差，后续将通过第五节所述的全局方法消除。

（一）扫描数据

子图构建是扫描坐标系与子图坐标系（以下简称坐标系）反复对齐的迭代过程。设扫描数据的原点为 $0\in {\mathbb{R}}^2$ ，扫描点信息表示为 $H=\{h_k{\}}_{k=1,...,K},(h_k\in {\mathbb{R}}^2)$。扫描坐标系在子图坐标系中的位姿 $\xi$ 通过变换矩阵 $T_{\xi }$ 表示，该矩阵将扫描点从扫描坐标系刚性变换至子图坐标系，其数学定义为：

$$T_p=\left(\begin{array}{cc}\cos {\xi }_{\theta }& -\sin {\xi }_{\theta }\\ \sin {\xi }_{\theta }& \cos {\xi }_{\theta }\end{array}\right)p+\left(\begin{array}{c}{\xi }_x\\ {\xi }_y\end{array}\right)$$

（二）子图

子图由多帧连续扫描数据构建，采用概率栅格形式表示，即：

$$M:r\mathbb{Z}\times r\mathbb{Z}\to [p_{\text{min}},p_{\text{max}}]$$

其中 $r$ 为分辨率（例如 5cm），该栅格将离散栅格点映射为概率值，表示栅格点被遮挡的概率。每个栅格点对应的像素包含所有距离该栅格点最近的空间点。

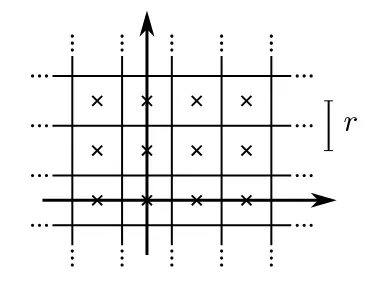
图 1. 栅格点及其相关像素

当将扫描数据插入概率栅格时，需计算命中点（hits）和未命中点（misses）对应的两组不相交栅格点集合：

• 对于每个命中点，将最近的栅格点加入命中集合；
• 对于每个未命中点，将扫描原点与扫描点之间射线相交的每个像素对应的栅格点（已在命中集合中的除外）加入未命中集合；
• 对于所有先前未观测的栅格点，若属于命中集合则赋值为 $P_{\text{hit}}$ ，若属于未命中集合则赋值为 $p_{\text{miss}}$；
• 若栅格点 $x$ 已被观测到，我们将命中和未命中的概率更新为：

$$odds(p)=\frac{p}{1-p}$$$$M_{new}(x)=clamp(odd{s}^{-1}(odds(M_{old}(x))\cdot odds(p_{hit})))$$

• 对于未命中的点也类似。

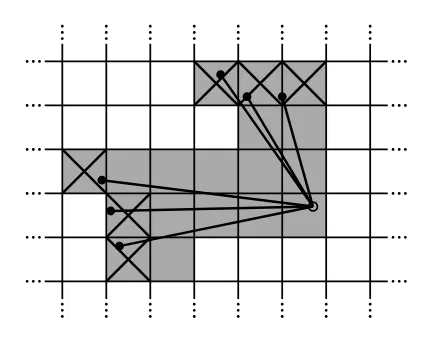
图 2. 扫描结果以及与命中（阴影部分已划掉）和未命中（仅阴影部分）相关的像素。

（三）Ceres 扫描匹配

在将扫描数据插入子图之前，利用基于 Ceres 求解器^[14]的扫描匹配器，相对于当前局部子图优化扫描位姿$\xi$。扫描匹配器的目标是找到使子图中扫描点概率最大化的扫描位姿，该问题被转化为非线性最小二乘问题：

$$\begin{array}{}\text{(CS)}& \arg \underset{\xi }{min}\sum _{k=1}^K(1-M_{\text{smooth}}(T_{\xi }{h}_k){)}^2\end{array}$$

其中：

• $T_{\xi }$ 根据扫描位姿将 $h_k$ 从扫描坐标系变换至子图坐标系；
• 函数 $M_{\text{smooth}}:{\mathbb{R}}^2\to \mathbb{R}$ 是局部子图概率值的平滑版本，采用双三次插值计算，因此可能出现取值范围超出 $[0,1]$ 的情况，但被认为不会影响结果。

该平滑函数的数学优化精度通常高于栅格分辨率。由于这是局部优化，需要良好的初始估计：

• 可利用能够测量角速度的 IMU 估计位姿的旋转分量 $\theta$ ；
• 在无 IMU 的情况下，可采用更高频率的扫描匹配或像素级精确扫描匹配方法（尽管这会增加计算开销）。

五、回环检测

由于扫描数据仅与包含近期少数扫描帧的子图进行匹配，上述方法会缓慢累积误差。对于几十帧连续扫描数据，累积误差较小；对于更大空间，则通过构建多个小子图来处理。我们的方法遵循稀疏位姿调整（Sparse Pose Adjustment）^[2:2]的思路，优化所有扫描数据和子图的位姿——扫描数据插入时的相对位姿被存储在内存中，用于回环优化；当子图不再更新后，所有扫描与子图的组合都将被纳入回环检测考虑范围，后台运行扫描匹配器，若找到优匹配结果，则将对应的相对位姿添加到优化问题中。

（一）优化问题

与扫描匹配类似，回环优化也被表述为非线性最小二乘问题，便于添加残差项以融合额外数据。每几秒使用 Ceres 求解器^[14:1]求解以下优化问题：

$$\begin{array}{}\text{(SPA)}& \underset{{\mathrm{\Xi }}^m,{\mathrm{\Xi }}^s}{\arg min}\frac{1}{2}\sum _{ij}\rho \left(E^2({\xi }_i^m,{\xi }_j^s;{\mathrm{\Sigma }}_{ij},{\xi }_{ij})\right)\end{array}$$

其中：

• ${\mathrm{\Xi }}^m=\{{\xi }_i^m{\}}_{i=1,...,m}$ 表示子图在世界坐标系中的位姿，${\mathrm{\Xi }}^s=\{{\xi }_j^s{\}}_{j=1,...,n}$ 表示扫描数据在世界坐标系中的位姿；
• 约束条件包括相对位姿 ${\xi }_{ij}$ 及对应的协方差矩阵 ${\mathrm{\Sigma }}_{ij}$ ，对于子图 $i$ 和扫描 $j$，${\xi }_{ij}$ 描述了扫描在子图坐标系中的匹配位置；
• 协方差矩阵 ${\mathrm{\Sigma }}_{ij}$ 可通过文献^[15]的方法计算，或利用 Ceres 求解器的协方差估计功能结合公式 $(CS)$ 进行局部计算；
• $E$ 为约束对应的残差，计算方法如下：

$$E^2({\xi }_i^m,{\xi }_j^s;{\mathrm{\Sigma }}_{ij},{\xi }_{ij})=e({\xi }_i^m,{\xi }_j^s;{\xi }_{ij}{)}^T{\mathrm{\Sigma }}_{ij}^{-1}e({\xi }_i^m,{\xi }_j^s;{\xi }_{ij})$$$$e({\xi }_i^m,{\xi }_j^s;{\xi }_{ij})={\xi }_{ij}-\left(\begin{array}{c}{R}_{{\xi }_i^m}^{-1}(t_{{\xi }_i^m}-t_{{\xi }_j^s})\\ {\xi }_{i;\theta }^m-{\xi }_{j;\theta }^s\end{array}\right)$$

• 采用损失函数 $\rho$（例如Huber损失）降低异常值的影响——在局部对称环境（如办公室隔间）中，扫描匹配可能会向优化问题中引入错误约束，从而产生异常值，其他处理异常值的方法可参见文献^[16]。

（二）分支定界扫描匹配

我们的目标是找到像素级精确的最优匹配：

$$\begin{array}{}\text{(BBS)}& {\xi }^{\ast }=\arg \underset{\xi \in \mathcal{W}}{max}\sum _{k=1}^K{M}_{\text{nearest}}(T_{\xi }{h}_k)\end{array}$$

其中 $\mathcal{W}$ 为搜索窗口，$M_{\text{nearest}}$ 是将 $M$ 扩展至整个 ${\mathbb{R}}^2$ 的函数（通过先将输入值四舍五入到最近的栅格点，即将栅格点的值扩展至对应的像素），可通过公式 $(CS)$ 进一步提高匹配质量。

1. 步长选择

通过合理选择步长可提高效率。选择角步长 ${\delta }_{\theta }$ ，使得最大测距范围 $d_{\text{max}}$ 处的扫描点移动距离不超过一个像素的宽度 $r$ ，利用余弦定理推导步长计算公式：

$$d_{max}=\underset{k=1,...,K}{max}||h_k||$$$${\delta }_{\theta }=\arccos (1-\frac{r^2}{2d_{max}^2})$$

我们计算覆盖给定线性和角度搜索窗口大小的整数步长，例如 $W_x=W_y=7\text{m}$ ， $W_{\theta }={30}^{\circ }$，

$$w_x=\left[\frac{W_x}{r}\right],w_y=\left[\frac{W_y}{r}\right],w_{\theta }=\left[\frac{W_{\theta }}{{\delta }_{\theta }}\right].$$

得到以估计值 ${\xi }_0$ 为中心的有限搜索窗口集合 $\mathcal{W}$，

$$\bar{\mathcal{W}}=\{-w_x,...,w_x\}\times \{-w_y,...,w_y\}\times \{-w_{\theta },...,w_{\theta }\}$$$$\mathcal{W}=\{{\xi }_0+(r{j}_x,r{j}_y,{\delta }_{\theta }{j}_{\theta }):(j_x,j_y,j_{\theta })\in \bar{\mathcal{W}}\}$$

可以很容易地制定出一个简单的算法来找到 ${\delta }^{\ast }$，参考算法 1，但对于我们考虑的搜索窗口大小来说，它的速度太慢了。

算法 1：朴素扫描匹配算法（求解 $(BBS)$）

$$\begin{array}{rl}& \mathbf{\text{Algorithm 1}}\text{Naive algorithm for (BBS)}\\ & \mathit{best}\mathit{\_}\mathit{score}\leftarrow -\mathrm{\infty }\\ & \mathbf{\text{for }}{j}_x=-w_x\mathbf{\text{ to }}{w}_x\mathbf{\text{ do}}\\ & \mathbf{\text{for }}{j}_y=-w_y\mathbf{\text{ to }}{w}_y\mathbf{\text{ do}}\\ & \mathbf{\text{for }}{j}_{\theta }=-w_{\theta }\mathbf{\text{ to }}{w}_{\theta }\mathbf{\text{ do}}\\ & \mathit{score}\leftarrow \sum _{k=1}^K{M}_{\text{nearest}}(T_{{\xi }_0+(r{j}_x,r{j}_y,{\delta }_{\theta }{j}_{\theta })}{h}_k)\\ & \mathbf{\text{if }}\mathit{score}>\mathit{best}\mathit{\_}\mathit{score}\mathbf{\text{ then}}\\ & \mathit{match}\leftarrow {\xi }_0+(r{j}_x,r{j}_y,{\delta }_{\theta }{j}_{\theta })\\ & \mathit{best}\mathit{\_}\mathit{score}\leftarrow \mathit{score}\\ & \mathbf{\text{end if}}\\ & \mathbf{\text{end for}}\\ & \mathbf{\text{end for}}\\ & \mathbf{\text{end for}}\\ & \mathbf{\text{return }}\mathit{best}\mathit{\_}\mathit{score}\text{ and }\mathit{match}\text{ when set}\end{array}$$

2. 分支定界算法原理

我们采用 分支定界法（Branch-and-Bound） 来高效计算大搜索窗口内的最优位姿 ${\xi }^{\ast }$ ，其通用流程见算法 2。该方法最初由混合整数线性规划（Mixed Integer Linear Programs, MILP）领域提出^[17]，相关文献广泛（简要综述可参阅^[18]）。

算法 2：通用分支定界法

$$\begin{array}{rl}& \mathbf{\text{Algorithm 2}}\text{Generic branch and bound}\\ & \mathit{best}\mathit{\_}\mathit{score}\leftarrow -\mathrm{\infty }\\ & C\leftarrow C_0\\ & \mathbf{\text{while }}C\ne \mathrm{\varnothing }\mathbf{\text{ do}}\\ & \text{Select a node }c\in C\text{ and remove it from the set.}\\ & \mathbf{\text{if }}c\text{ is a leaf node}\mathbf{\text{ then}}\\ & \mathbf{\text{if }}\mathit{score}(c)>\mathit{best}\mathit{\_}\mathit{score}\mathbf{\text{ then}}\\ & \mathit{solution}\leftarrow n\\ & \mathit{best}\mathit{\_}\mathit{score}\leftarrow \mathit{score}(c)\\ & \mathbf{\text{end if}}\\ & \mathbf{\text{else}}\\ & \mathbf{\text{if }}\mathit{score}(c)>\mathit{best}\mathit{\_}\mathit{score}\mathbf{\text{ then}}\\ & \text{Branch: Split }c\text{ into nodes }{C}_c.\\ & C\leftarrow C\cup C_c\\ & \mathbf{\text{else}}\\ & \text{Bound.}\\ & \mathbf{\text{end if}}\\ & \mathbf{\text{end if}}\\ & \mathbf{\text{end while}}\\ & \mathbf{\text{return }}\mathit{best}\mathit{\_}\mathit{score}\text{ and }\mathit{solution}\text{ when set.}\end{array}$$

核心思想是将可能的解子集表示为树中的节点：

• 根节点（Root Node）：代表所有可能的解（本文中为 $\mathcal{W}$ ）；
• 子节点（Children Nodes）：对父节点解空间进行划分，其并集与父节点等价；
• 叶节点（Leaf Nodes）：为单元素集合，每个叶节点对应一个可行解；

该算法是精确的（exact），与暴力搜索（naive approach）结果一致，但要求内部节点 $c$ 的得分 $\text{score}(c)$ 必须是该节点所有子节点得分的上界（upper bound），若某节点的上界低于当前已知最优解，则可直接剪枝（bound），无需遍历该子树。

3. 算法实现细节

要实现具体算法，需确定节点选择（Node Selection）、分支策略（Branching）和上界计算方法（Upper Bound Computation）：

• 节点选择：决定搜索树的遍历顺序，默认采用深度优先搜索（DFS），在没有更优替代方案时，DFS 能够高效地剪枝（prune）大部分搜索树。该效率依赖于两个关键因素：
  1. 紧致的上界（Good Upper Bound）
  2. 高质量的当前解（Good Current Solution）

DFS 的优势在于能快速评估大量叶节点（leaf nodes），从而快速提供可行解。此外，为避免将低质量匹配误判为回环约束（loop closing constraints），我们引入得分阈值（score threshold），仅对超过该阈值的解感兴趣。实践中，由于多数情况下得分难以超过阈值，因此节点选择策略或初始启发式解的优先级相对降低。

DFS 子节点访问顺序，我们按以下策略访问子节点：

1. 计算每个子节点的得分上界（upper bound）。
2. 优先访问上界最大（most promising）的子节点，以加速剪枝。

该方法的伪代码实现见算法 3。

算法 3：DFS分支定界扫描匹配器（求解 $(BBS)$）

$$\begin{array}{rl}& \mathbf{\text{Algorithm 3}}\text{DFS branch and bound scan matcher for (BBS)}\\ & \mathit{best}\mathit{\_}\mathit{score}\leftarrow \text{score\_threshold}\\ & \text{Compute and memorize a score for each element in }{C}_0.\\ & \text{Initialize a stack }C\text{ with }{C}_0\text{ sorted by score, the maximum score at the top.}\\ & \mathbf{\text{while }}C\text{ is not empty}\mathbf{\text{ do}}\\ & \text{Pop }c\text{ from the stack }C.\\ & \mathbf{\text{if }}\mathit{score}(c)>\mathit{best}\mathit{\_}\mathit{score}\mathbf{\text{ then}}\\ & \mathbf{\text{if }}c\text{ is a leaf node}\mathbf{\text{ then}}\\ & \mathit{match}\leftarrow {\xi }_c\\ & \mathit{best}\mathit{\_}\mathit{score}\leftarrow \mathit{score}(c)\\ & \mathbf{\text{else}}\\ & \text{Branch: Split }c\text{ into nodes }{C}_c.\\ & \text{Compute and memorize a score for each element in }{C}_c.\\ & \text{Push }{C}_c\text{ onto the stack }C,\text{ sorted by score, the maximum score last.}\\ & \mathbf{\text{end if}}\\ & \mathbf{\text{end if}}\\ & \mathbf{\text{end while}}\\ & \mathbf{\text{return }}\mathit{best}\mathit{\_}\mathit{score}\text{ and }\mathit{match}\text{ when set.}\end{array}$$

• 分支规则：树中的每个节点由整数元组 $c=(c_x,c_y,c_{\theta },c_h)\in {\mathbb{Z}}^4$ 描述。

对于层级高度为 $c_h$ 的节点，其覆盖的候选解空间定义为：

$${\overline{\stackrel{―}{\mathcal{W}}}}_c=(\{(j_x,j_y)\in {\mathbb{Z}}^2:\begin{array}{c}{c}_x\le j_x<c_x+2^{c_h}\\ c_y\le j_y<c_y+2^{c_h}\end{array}\}\times \left\{c_{\theta }\right\})$$$${\bar{\mathcal{W}}}_c={\overline{\stackrel{―}{\mathcal{W}}}}_c\cap \bar{\mathcal{W}}$$

每个非叶节点包含最多 $2^{c_h}\times 2^{c_h}$ 个可能的平移位置，节点固定表示特定旋转角度 $c_{\theta }$。

当 $c_h=0$ 时到达叶节点，对应可行解 $\bar{\mathcal{W}}\ni {\xi }_c={\xi }_0+(r{c}_x,r{c}_y,{\delta }_{\theta }{c}_{\theta })$。

在算法 3的具体实现中，包含所有可行解的根节点并不显式出现，而是直接分支为一组初始节点 $C_0$​。这些初始节点位于固定高度 $h_0$​，覆盖整个搜索窗口：

搜索窗口在三个维度上的离散化表示为：

$$\begin{array}{rl}{\bar{\mathcal{W}}}_{0,x}& =\{-w_x+2^{h_0}{j}_x:j_x\in \mathbb{Z},0\le 2^{h_0}{j}_x\le 2w_x\}\\ {\bar{\mathcal{W}}}_{0,y}& =\{-w_y+2^{h_0}{j}_y:j_y\in \mathbb{Z},0\le 2^{h_0}{j}_y\le 2w_y\}\\ {\bar{\mathcal{W}}}_{0,\theta }& =\{j_{\theta }\in \mathbb{Z}:-w_{\theta }\le j_{\theta }\le w_{\theta }\}\end{array}$$

初始节点集合为这些维度的笛卡尔积：

$$C_0={\bar{\mathcal{W}}}_{0,x}\times {\bar{\mathcal{W}}}_{0,y}\times {\bar{\mathcal{W}}}_{0,\theta }\times \{h_0\}$$

对于 $c_h>1$ 的任意节点 $c$ ，最多生成4个高度为 $c_h-1$ 的子节点。

$$C_c=((\{c_x,c_x+2^{c_h-1}\}\times \{c_y,c_y+2^{c_h-1}\}\times c_{\theta })\cap \bar{\mathcal{W}})\times \{c_h-1\}$$

• 上界计算（Computing Upper Bounds）：在分支定界法中，关键步骤是高效计算内部节点的上界。我们采用以下方法：

$$\begin{array}{rl}\text{score}(c)& =\sum _{k=1}^K\underset{j\in {\overline{\stackrel{―}{\mathcal{W}}}}_c}{max}{M}_{\text{nearest}}\left(T_{{\xi }_j}{h}_k\right)\\ & \ge \sum _{k=1}^K\underset{j\in {\bar{\mathcal{W}}}_c}{max}{M}_{\text{nearest}}\left(T_{{\xi }_j}{h}_k\right)\\ & \ge \underset{j\in {\bar{\mathcal{W}}}_c}{max}\sum _{k=1}^K{M}_{\text{nearest}}\left(T_{{\xi }_j}{h}_k\right)\end{array}$$

为高效计算最大值，我们引入预计算栅格 $M_{\text{precomp}}^{c_h}$ ，为每个可能的高度 $c_h$ 预计算一个栅格，使得得分计算的时间复杂度与扫描点数量呈线性关系。需注意，为此我们需要计算 ${\overline{\stackrel{―}{\mathcal{W}}}}_c$ 上的最大值，该范围可能在搜索空间边界附近大于 ${\bar{\mathcal{W}}}_c$ 。

$$\text{score}(c)=\sum _{k=1}^K{M}_{\text{precomp}}^{c_h}(T_{{\xi }_c}{h}_k)$$$$M_{\text{precomp}}^h(x,y)=\underset{\begin{array}{c}{x}^{\prime }\in [x,x+r(2^h-1)]\\ y^{\prime }\in [y,y+r(2^h-1)]\end{array}}{max}{M}_{\text{nearest}}(x^{\prime },y^{\prime })$$

其中 ${\xi }_c$ 与叶节点定义相同。

$M_{\text{precomp}}^h$ 与 $M_{\text{nearest}}$ 具有相同的像素结构，但每个像素存储从该像素开始的 $2^h\times 2^h$ 像素块的最大值。

图 3 展示了此类预计算栅格的示例。

图 3. 预先计算的大小为 1、4、16 和 64 的栅格。

为降低预计算栅格的计算量，我们等待概率栅格（probability grid）不再接收更新后才进行计算。随后，我们会计算一组预计算栅格（precomputed grids），并开始与之进行匹配。

对于每个预计算栅格，我们计算从每个像素开始，宽度为 $2^h$ 像素的行内最大值。利用该中间结果，迭代构建下一个预计算栅格。

若按照添加顺序移除值，则动态集合的最大值可在摊消 $O(1)$ 的时间内更新。连续的最大值存储在一个双端队列中，该队列可以递归地定义为，包含当前集合中所有值的最大值，以及从该最大值首次出现之后所有值的连续最大值列表。对于空值集合，此列表为空。使用这种方法，预计算栅格的计算时间复杂度为 $O(n)$ ，其中 $n$ 是每个预计算栅格中的像素数。

另一种上界计算方法是计算较低分辨率的概率栅格，逐级减半分辨率（如文献^[1:2]所述）。由于本方法的内存开销可控，我们优先选择它而非低分辨率栅格，后者会产生比式(15)更差的边界，从而降低性能。

六、实验结果

本节展示了我们基于记录的传感器数据计算得到的SLAM算法结果，这些计算使用了与背包设备上交互运行时相同的在线算法。首先，我们展示了使用 Cartographer 背包在慕尼黑德意志博物馆采集的传感器数据结果；其次，通过使用扫地机器人采集的传感器数据，证明我们的算法在廉价硬件上同样表现良好；最后，我们展示了采用Radish数据集^[19]的实验结果，并与已发表的研究成果进行了对比。

（一）真实场景实验：德意志博物馆

利用在德意志博物馆采集的传感器数据（数据时长1913s，计算得到的轨迹长度2253m），生成对应的地图。在配备Intel Xeon E5-1650（3.2GHz）处理器的工作站上，我们的SLAM算法CPU总耗时为1018s，内存占用最高2.2GB，最多使用4个后台线程进行回环扫描匹配。其实际运行时间为360s，这意味着它的实时性能达到了5.3倍。

用于回环优化的生成图包含11456个节点和35300条边。每当向图中添加几个节点时，就会执行一次稀疏位姿调整（SPA）优化，典型的优化过程需3次迭代，耗时约0.3s。

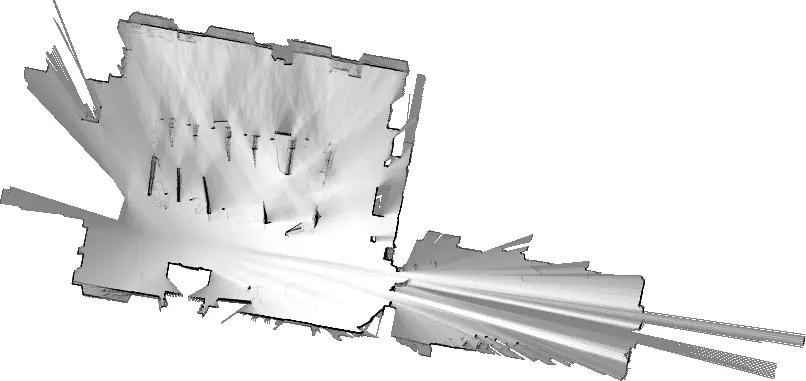
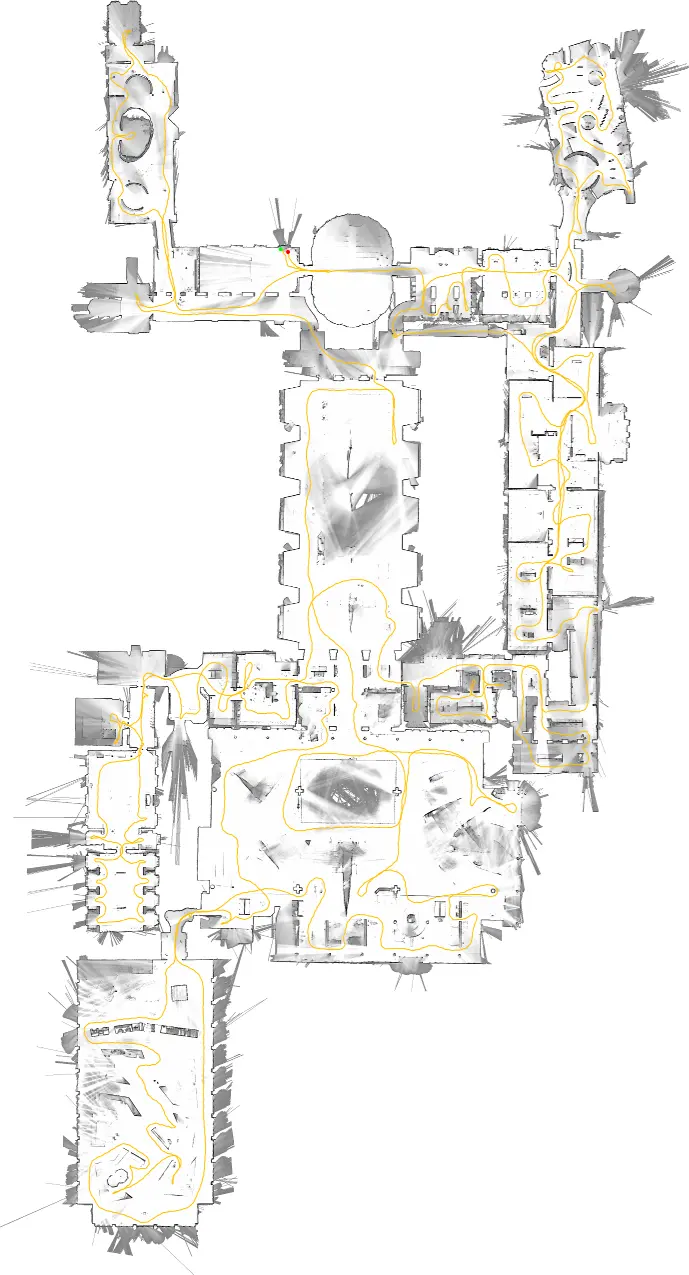图 4. 德意志博物馆二楼的 Cartographer 地图。

（二）真实场景实验：Neato Revo激光雷达

Neato Robotics 公司在其扫地机器人中采用了一款成本低于 30 美元的激光测距传感器 Revo LDS^[20]。我们通过将扫地机器人放在手推车上四处移动来采集数据，同时通过调试接口控制扫地机器人以约 2Hz 的频率进行扫描，图 5展示了生成的 5cm 分辨率平面图。为评估该平面图质量，我们将 5 条直线的激光卷尺测量结果与地图中通过绘图工具计算的像素距离进行对比，结果如表 1所示（所有数值单位为米）。这些数值大致处于每条线两端各一个像素的预期数量级范围内。

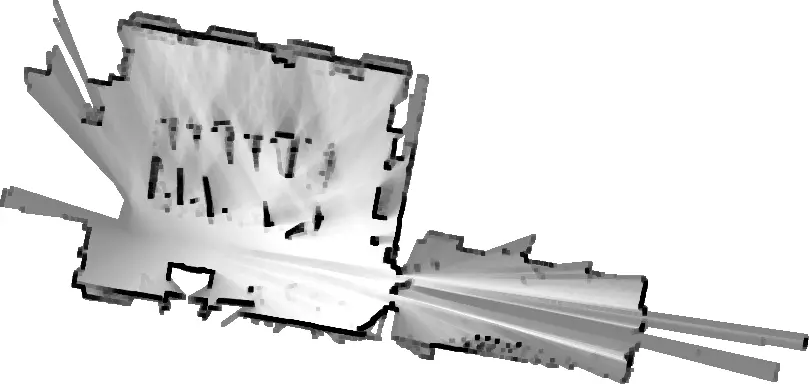
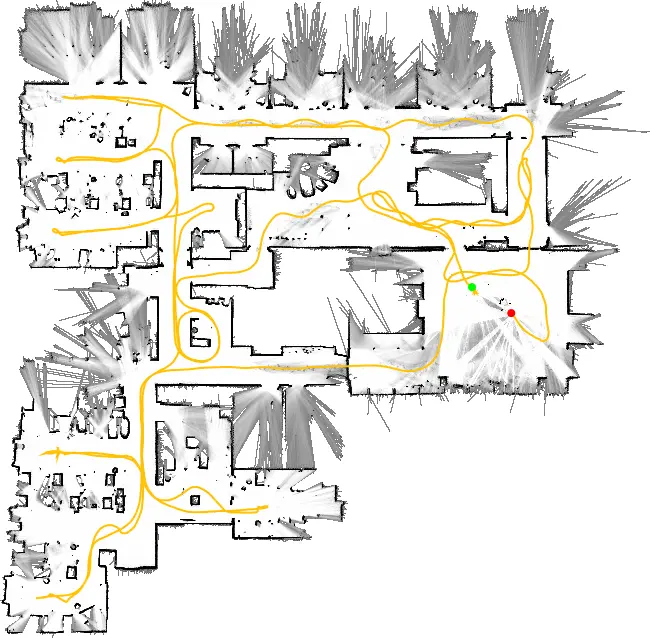图 5. 使用 Revo LDS 传感器数据生成的 Cartographer 地图。

表 1. Revo LDS 的定量误差

激光测距值	Cartographer 测量值	绝对误差	相对误差
4.09	4.08	-0.01	-0.2%
5.40	5.43	+0.03	+0.6%
8.67	8.74	+0.07	+0.8%
15.09	15.20	+0.11	+0.7%
15.12	15.23	+0.11	+0.7%

（三）基于Radish数据集的对比

我们使用文献^[21]中建议的基准度量方法，将我们的方法与其他方法进行对比。该方法将相对位姿变化的误差与人工整理的真值关系进行对比。表 2展示了通过我们 Cartographer SLAM 算法计算得到的结果。为便于比较，我们引用了文献^[21:1]中关于图映射（Graph Mapping, GM）的结果。此外，我们在表 3中引用了文献^[9:1]中最新发表的结果。所有误差均以米和度作为单位，包括绝对误差或平方误差，以及它们的标准差。

每个公开数据集都是通过独特的传感器配置收集的，这与我们的 Cartographer 背包不同。因此，需要调整各种算法参数以产生合理的结果。根据我们的经验，调整 Cartographer 仅需使算法与传感器配置相匹配，而无需适配特定环境。

由于每个公开数据集都有独特的传感器配置，我们无法确定我们有没有将参数也拟合到特定位置。唯一的例外是弗莱堡医院（Freiburg hospital）数据集，该数据集有两个独立的关系文件。我们使用局部关系调整了参数，但在全局关系上也看到了良好的结果。所有数据集之间最显著的差异在于激光扫描的频率与质量，以及里程计的可用性与精度。

表 2. 与文献^[21:2]中图映射（GM）方法的对比

场景	指标	Cartographer	GM
Aces	绝对平移误差（m）	0.0375±0.0426	0.044±0.044
	平方平移误差（m²）	0.0032±0.0285	0.004±0.009
	绝对旋转误差（°）	0.373±0.469	0.4±0.4
	平方旋转误差（°²）	0.359±3.696	0.3±0.8
Intel	绝对平移误差（m）	0.0229±0.0239	0.031±0.026
	平方平移误差（m²）	0.0011±0.0040	0.002±0.004
	绝对旋转误差（°）	0.453±1.335	1.3±4.7
	平方旋转误差（°²）	1.986±23.988	24.0±166.1
MIT Killian Court	绝对平移误差（m）	0.0395±0.0488	0.050±0.056
	平方平移误差（m²）	0.0039±0.0144	0.006±0.029
	绝对旋转误差（°）	0.352±0.353	0.5±0.5
	平方旋转误差（°²）	0.248±0.610	0.9±0.9
MIT CSAIL	绝对平移误差（m）	0.0319±0.0363	0.004±0.009
	平方平移误差（m²）	0.0023±0.0099	0.0001±0.0005
	绝对旋转误差（°）	0.369±0.365	0.05±0.08
	平方旋转误差（°²）	0.270±0.637	0.01±0.04
Freiburg bldg 79	绝对平移误差（m）	0.0452±0.0354	0.056±0.042
	平方平移误差（m²）	0.0033±0.0055	0.005±0.0005
	绝对旋转误差（°）	0.538±0.718	0.6±0.6
	平方旋转误差（°²）	0.804±3.627	0.7±1.7
Freiburg hospital (local)	绝对平移误差（m）	0.1078±0.1943	0.143±0.180
	平方平移误差（m²）	0.0494±0.2831	0.053±0.272
	绝对旋转误差（°）	0.747±2.047	0.9±2.2
	平方旋转误差（°²）	4.745±40.081	5.5±46.2
Freiburg hospital (global)	绝对平移误差（m）	5.2242±6.6230	11.6±11.9
	平方平移误差（m²）	71.0288±267.7715	276.1±516.5
	绝对旋转误差（°）	3.341±4.797	6.3±6.2
	平方旋转误差（°²）	34.107±127.227	77.2±154.8

表 3. 与文献^[9:2]中Graph FLIRT方法的对比

场景	指标	Cartographer	Graph FLIRT
Intel	绝对平移误差（m）	0.0229±0.0239	0.02±0.02
	绝对旋转误差（°）	0.453±1.335	0.3±0.3
Freiburg bldg 79	绝对平移误差（m）	0.0452±0.0354	0.06±0.09
	绝对旋转误差（°）	0.538±0.718	0.8±1.1
Freiburg hospital (local)	绝对平移误差（m）	0.1078±0.1943	0.18±0.27
	绝对旋转误差（°）	0.747±2.047	0.9±2.0
Freiburg hospital (global)	绝对平移误差（m）	5.2242±6.6230	8.3±8.6
	绝对旋转误差（°）	3.341±4.797	5.0±5.3

表 4. 回环检测精度

测试案例	约束数量	精度
Aces	971	98.1%
Intel	5786	97.2%
MIT Killian Court	916	93.4%
MIT CSAIL	1857	94.1%
Freiburg bldg 79	412	99.8%
Freiburg hospital	554	77.3%

表 5. 性能指标

测试案例	数据时长（s）	实际运行时间（s）
Aces	1366	41
Intel	2691	179
MIT Killian Court	7678	190
MIT CSAIL	424	35
Freiburg bldg 79	1061	62
Freiburg hospital	4820	10

尽管公开数据集使用的传感器硬件相对陈旧，但 Cartographer SLAM 系统的表现始终符合预期，即使在 MIT CSAIL 数据集上（其表现显著落后于 Graph Mapping 算法）。在 Intel 数据集上，我们的表现优于 Graph Mapping ，但不及 Graph FLIRT ；在 MIT Killian Court 数据集上，我们的所有指标均超越 Graph Mapping ；其余所有案例中， Cartographer 在大多数（但非全部）指标上超越 Graph Mapping 和 Graph FLIRT 。

由于我们在子图与扫描之间添加了回环闭合约束，这些约束缺乏真实值参考，且难以与其他基于"扫描-扫描匹配"的方法进行数值比较。表 4列出了各测试案例中添加的回环闭合约束数量（包括正确与误报），以及准确率（即正确约束占比）。我们将真实正确约束定义为：在计算稀疏位姿调整（SPA）时，偏移不超过 20 厘米或 1° 的所有回环闭合约束子集。实验表明，尽管"扫描-子图匹配"过程会产生需要 SPA 优化处理的误报，但在所有测试案例中都能提供足够的回环闭合约束。SPA中采用Huber损失函数是增强回环闭合抗干扰能力的关键因素之一。

在弗莱堡医院数据集中，由于选择较低分辨率和回环检测最低分数阈值，导致误报率相对较高。虽然提高最低分数阈值可提升准确率，但根据真实值检验，这会降低某些维度的求解质量。作者认为真实值仍是评估最终地图质量的更优基准。

Cartographer SLAM 的参数未针对 CPU 性能进行调优。表 5仍提供了在 Intel Xeon E5-1650 3.2GHz 工作站上测量的运行耗时，并附传感器数据持续时间作为参照。

七、结论

本文提出并通过实验验证了一种结合"扫描-子图匹配"、回环检测与图优化的二维 SLAM 系统。我们采用基于栅格的局部SLAM方法构建独立的子图轨迹。在后台处理中，所有扫描数据均通过像素级精度的扫描匹配与邻近子图对齐，从而生成回环闭合约束。子图与扫描位姿构成的约束图会在后台周期性进行优化。操作者可实时获取由已完成子图与当前子图经 GPU 加速合成的最新地图预览。实验证明，我们的算法能够在普通硬件配置上实现实时运行。

致谢

本研究通过在慕尼黑德意志博物馆的实验得到验证，作者感谢博物馆管理层对本项工作的支持。对比实验采用了人工验证的关联数据及文献^[21:3]的结果（该文献使用了机器人数据集存储库 Radish^[19:1]的数据）。感谢 Patrick Beeson、Dieter Fox、Dirk Hähnel、Mike Bosse、John Leonard 以及 Cyrill Stachniss 提供这些数据。弗莱堡大学医院的数据由 Bastian Steder、Rainer Kümmerle、Christian Dornhege、Michael Ruhnke、Cyrill Stachniss、Giorgio Grisetti 和 Alexander Kleiner 提供。

贡献者

Cody Gu

页面历史

最后编辑于 1 分钟前

查看完整历史

3c43d60-docs: 添加oerv荔枝派WiFi驱动教程

---

1. Olson E. M3RSM: Many-to-many multi-resolution scan matching[C]//2015 IEEE international conference on robotics and automation (ICRA). IEEE, 2015: 5815-5821. ↩︎ ↩︎ ↩︎

2. Konolige K, Grisetti G, Kümmerle R, et al. Efficient sparse pose adjustment for 2D mapping[C]//2010 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2010: 22-29. ↩︎ ↩︎ ↩︎

3. Lu F, Milios E. Globally consistent range scan alignment for environment mapping[J]. Autonomous robots, 1997, 4(4): 333-349. ↩︎

4. Martín F, Triebel R, Moreno L, et al. Two different tools for three-dimensional mapping: DE-based scan matching and feature-based loop detection[J]. Robotica, 2014, 32(1): 19-41. ↩︎ ↩︎

5. Kohlbrecher S, Von Stryk O, Meyer J, et al. A flexible and scalable SLAM system with full 3D motion estimation[C]//2011 IEEE international symposium on safety, security, and rescue robotics. IEEE, 2011: 155-160. ↩︎

6. Himstedt M, Frost J, Hellbach S, et al. Large scale place recognition in 2D LIDAR scans using geometrical landmark relations[C]//2014 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2014: 5030-5035. ↩︎

7. Granström K, Schön T B, Nieto J I, et al. Learning to close loops from range data[J]. The international journal of robotics research, 2011, 30(14): 1728-1754. ↩︎

8. Grisetti G, Stachniss C, Burgard W. Improving grid-based slam with rao-blackwellized particle filters by adaptive proposals and selective resampling[C]//Proceedings of the 2005 IEEE international conference on robotics and automation. IEEE, 2005: 2432-2437. ↩︎

9. Tipaldi G D, Braun M, Arras K O. FLIRT: Interest regions for 2D range data with applications to robot navigation[C]//Experimental Robotics: The 12th International Symposium on Experimental Robotics. Berlin, Heidelberg: Springer Berlin Heidelberg, 2014: 695-710. ↩︎ ↩︎ ↩︎

10. Strom J, Olson E. Occupancy grid rasterization in large environments for teams of robots[C]//2011 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2011: 4271-4276. ↩︎

11. Kümmerle R, Grisetti G, Strasdat H, et al. g 2 o: A general framework for graph optimization[C]//2011 IEEE international conference on robotics and automation. IEEE, 2011: 3607-3613. ↩︎

12. Carlone L, Aragues R, Castellanos J A, et al. A fast and accurate approximation for planar pose graph optimization[J]. The International Journal of Robotics Research, 2014, 33(7): 965-987. ↩︎

13. Bosse M, Zlot R. Map matching and data association for large-scale two-dimensional laser scan-based slam[J]. The International Journal of Robotics Research, 2008, 27(6): 667-691. ↩︎

14. Agarwal S, Mierle K, et al. Ceres solver[EB/OL]. http://ceres-solver.org. ↩︎ ↩︎

15. Olson E B. Real-time correlative scan matching[C]//2009 IEEE international conference on robotics and automation. IEEE, 2009: 4387-4393. ↩︎

16. Agarwal P, Tipaldi G D, Spinello L, et al. Robust map optimization using dynamic covariance scaling[C]//2013 IEEE international conference on robotics and automation. Ieee, 2013: 62-69. ↩︎

17. Land A H, Doig A G. An automatic method for solving discrete programming problems[M]//50 Years of Integer Programming 1958-2008: From the Early Years to the State-of-the-Art. Berlin, Heidelberg: Springer Berlin Heidelberg, 2009: 105-132. ↩︎

18. Clausen J. Branch and bound algorithms-principles and examples[J]. Department of computer science, University of Copenhagen, 1999: 1-30. ↩︎

19. Howard A, Roy N. The robotics data set repository (Radish)[EB/OL]. 2003. http://radish.sourceforge.net/. ↩︎ ↩︎

20. Konolige K, Augenbraun J, Donaldson N, et al. A low-cost laser distance sensor[C]//2008 IEEE international conference on robotics and automation. IEEE, 2008: 3002-3008. ↩︎

21. Kümmerle R, Steder B, Dornhege C, et al. On measuring the accuracy of SLAM algorithms[J]. Autonomous Robots, 2009, 27(4): 387-407. ↩︎ ↩︎ ↩︎ ↩︎